10432. Многоугольник в окружности
Правильный многоугольник вписан в
окружность. По заданному радиусу окружности и количеству сторон вычислить
площадь многоугольника.
Вход.
Каждая строка является отдельным тестом и содержит радиус окружности r (0 < r < 20000)
и количество сторон многоугольника n (2 < n < 20000).
Выход. Для каждого теста вывести в отдельной строке
площадь многоугольника.
Пример входа
2 200010 3000
Пример выхода
12.566
314.159
РЕШЕНИЕ
геометрия
Анализ алгоритма
Пусть
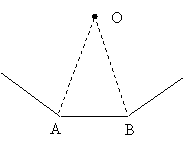
А и В – последовательные вершины многоугольника, О – центр описанной
окружности. Поскольку многоугольник имеет n сторон, то угол AOB равен 2p / n. Площадь треугольника AOB равна ½ * AO * OB * sin ÐAOB = ½ * r2 * sin(2p/n). Площадь исходного многоугольника равна n * SAOB = ½ * n * r2 * sin(2p/n).
Пример
Для первого теста площадь
многоугольника, округленная до трех знаков после запятой, равна ½ * 2000 * 22 * sin(2p/2000) =
12.566.
Реализация алгоритма
Объявим константу p.
#define PI 2*acos(0.0)
Для каждой пары вычисляем площадь многоугольника по выше
приведенной формуле и выводим ее с тремя знаками после запятой.
while (scanf("%lf
%lf",&r,&n) == 2)
{
res = n * r * r * sin(2.0*PI/n)/2;
printf("%.3lf\n",res);
}